编译器工作的基本原理1

XiLaiTL大约 12 分钟

编译器工作的基本原理1

书接上回：

终结符是什么？
词法分析是什么？
语法分析是什么？
编译器的运行流程是什么？
语法树是什么？

编译器和解释器

我们可以用一个函数来定义编译器和解释器：

Compiler : (String)->String = 用宿主语言写的，从源语言字符串到目标语言字符串的一个函数。
Interpreter : (String)->Result = 用宿主语言写的，将源语言字符串解释执行得到结果的一个函数。

编译器的主要流程，就是如何读取源语言的形式化文本，如何根据规定的操作，转化为目标语言字符串。因此Compiler函数是由许多个函数复合而成的，这些函数在传递的时候不一定都是字符串进行传递。

我们定义一个管道运算符更简洁地表示函数的复合情况：

A |> Func === Func(A)
A |> B |> Func === Func(B(A))

就像函数可以进行复合，编译器也是可以进行组合的。

我们可以认为汇编指令集是一个跑在CPU上的解释器，那么传统编译器如C语言编译器到运行时的步骤可以被描述为：

//形式化文本
type C_Code = String;
type ARM_Code = String;

//编译器和解释器
fun C_Compiler : (C_Code)->ARM_Code;
fun ARM_V8 : (ARM_Code)->Result;

//运行
code |> C_Compiler |> ARM_V8 

//最终得到Result

解释器的工作流程

从我们定义的Expr解释器的工作文件Main.kt，我们可以看到：

type Code = String

fun CharStreams.fromString : (Code)->CharStream
fun Lexer.constructor : (CharStream)->Lexer
fun CommonTokenStream.constructor : (Lexer)->TokenStream
fun Parser.constructor : (TokenStream)->Parser
fun Parser.prog : ()->ParseTree
fun Visitor.constructor: ()->Visitor
fun Visitor.visit: (ParseTree)->Result

//为了好看，稍微调整一下函数
fun prog : (Parser)->ParseTree

result = code |> CharStreams.fromString |> Lexer |> CommonTokenStream |> Parser |> prog |> Visitor().visit

我们的解释器的工作流程，果然是一个从源语言字符串到运行结果的函数！

可以对照着上一节的流程图上观察一下流程

处理形式化文本需要的步骤

给定一系列字符串，我们要怎么知道这句话或者这段文字的含义呢？

词法分析

第一步要做的事情就是——分析这段文字的语素；或者说，单词；或者说，最小不可分隔的语法单元。这样的单词在形式文法中被称为“终结符”（Terminal）。

什么规则下的字符可以组成最小不可分隔的语法单元呢？以C语言为例子，看如下字面量：

int main(){
    int i=0;
    i++;
    return 0;
}

是不是可以分成以下几个类型？

关键字：int return
常数：0
标识符：main i
运算符：++ =
界限符：; ( ) { }

除了关键字以外，值得注意的是，main是也作为一个单词整体存在的，也就是说，连续字母应该被视为单词。

很显然，如果我们要处理一段文本，我们不仅要获得每个单词片段，我们还需要知道单词代表的含义，也就是单词的类型。这种由单词片段以及该片段的属性组合而成的结构，叫做属性字（Token）。

$属性字：{单词属性;单词值}$

这就是词法分析需要完成的内容——从字符串中分隔单词，并归类。

插播：文法规则

那要如何进行归类呢？我们有一个很朴素的想法：通过正则表达式可以识别并匹配字符串。

为什么正则表达式可以识别并匹配字符串呢？因为正则表达式等价于自动机（现代编程语言的正则表达式能力强于自动机），而自动机则可以识别字符串。

自动机是怎么识别字符串的呢？这里写一个模拟自动机运行程序：

这样的程序可以识别到诸如abccccde或者abccccf的字符串。

var ch = nextChar()
while(state!=-1){
    when(state){
        0-> if (ch == 'a'){
            ch = nextChar()
            state = 1
        }
        1-> if (ch == 'b'){
            ch = nextChar()
            state = 2
        }
        TODO()
    }
}

像这样子，完成一个自动机程序，即可做到字符串的识别。

一个正则表达式描述不全所有类型的单词，我们需要引入多个正则表达式；而一种类型规则很有可能是有多个正则规则组合而成的。

BNF文法表示

因此我们用文法表示来描述一个语言的文法规则，而不仅仅是词法规则。

通常，我们使用巴科斯范式（BNF，Backus-Naur Form）来描述语言的文法规则。BNF表示语法规则的方式为：

非终结符用尖括号括起
每条规则的
- 左部是一个非终结符
- 右部是由非终结符和终结符组成的一个符号串（称为候选式）
- 中间一般以“：：=”或者“->”分开
具有相同左部的规则可以共用一个左部，各右部之间以直竖“|”隔开。

其中，非终结符指的是，由终结符规则组合而成的文法符号。以自然语言文本为例：

<句子>::=<主语><谓语>
<主语>::=<形容词><名词>
<谓语>::=<动词><宾语>
<宾语>::=<形容词><名词>
<形容词>::=大|小
<动词>::=吃
<名词>::=花生|八哥

试试通过文法规则匹配小八哥吃大花生吧！。

我们观察一下Python官方文档的巴科斯范式表示 2. 词法分析 — Python 3.12.2 文档open in new window

integer      ::=  decinteger | bininteger | octinteger | hexinteger
decinteger   ::=  nonzerodigit (["_"] digit)* | "0"+ (["_"] "0")*
bininteger   ::=  "0" ("b" | "B") (["_"] bindigit)+
octinteger   ::=  "0" ("o" | "O") (["_"] octdigit)+
hexinteger   ::=  "0" ("x" | "X") (["_"] hexdigit)+
nonzerodigit ::=  "1"..."9"
digit        ::=  "0"..."9"
bindigit     ::=  "0" | "1"
octdigit     ::=  "0"..."7"
hexdigit     ::=  digit | "a"..."f" | "A"..."F"

可以了解到的是，我们可以在BNF式右侧引入正则表达式的一些规则来简化描述。因此，增强版本的BNF式加入了一些通用的规则。

[]代表可选
"1"..."9"代表1到9的字符
+代表1个或者多个
*代表0个或者多个

ANTLR的词法规则

在ANTLR中，BNF范式的语法形式有所不同，并且区分词法规则与文法规则。

语法规则：描述非终结符的组合规则
词法规则：描述终结符的类型规则

//以下是语法规则：描述非终结符的组合规则
<句子>::=<主语><谓语>
<主语>::=<形容词><名词>
<谓语>::=<动词><宾语>
<宾语>::=<形容词><名词>

//以下是词法规则：描述终结符的类型规则
<形容词>::=大|小
<动词>::=吃
<名词>::=花生|八哥

ANTLR词法规则的主要形式如下：

词法规则的匹配结果是终结符
词法规则首字母要大写；
词法规则使用到的式子只能是字符或者词法片段（fragment开头），不能是其他词法规则；
词法片段仅用于词法规则中，不会被当作终结符；
[]表示括号内部的字符选其一，[0-9]表示从0到9的字符选其一；+代表1个或者多个；*代表0个或者多个；?代表0个或1个

INTEGER : DECIMAL_INTEGER | OCT_INTEGER | HEX_INTEGER | BIN_INTEGER;
DECIMAL_INTEGER : NON_ZERO_DIGIT DIGIT* | '0'+ ;
OCT_INTEGER : '0' [oO] OCT_DIGIT+ ;
HEX_INTEGER : '0' [xX] HEX_DIGIT+ ;
BIN_INTEGER : '0' [bB] BIN_DIGIT+ ;

fragment NON_ZERO_DIGIT : [1-9];
fragment DIGIT : [0-9];
fragment OCT_DIGIT : [0-7];
fragment HEX_DIGIT : [0-9a-fA-F];
fragment BIN_DIGIT : [01];

语法分析

从词法分析处获得字符串文本段的属性字流后，我们就可以进行这些属性字的组合分析了，也就是说，分析出单词组合而成的句型。

语法树

同样，我们依然可以用文法表示来描述语法规则。

回顾我们的Expr计算器解释器：

grammar Expr;
//以下是语法规则
prog:   (expr NEWLINE)* ;
expr:   expr op=('*'|'/') expr
    |   expr op=('+'|'-') expr
    |   INT
    |   '(' expr ')'
    ;
    
//以下是词法规则
NEWLINE : [\r\n]+ ;
INT     : [0-9]+ ;

观察语法规则，我们可以发现——如果排除掉递归形式，语法规则可以被描述为，以入口规则为根节点的一颗树。当每个节点都被记录上规则时，我们可以展开递归——一段字符串文本就可以用一棵树来描述了！还记得我们之前通过ANTLR插件观察的树吗？

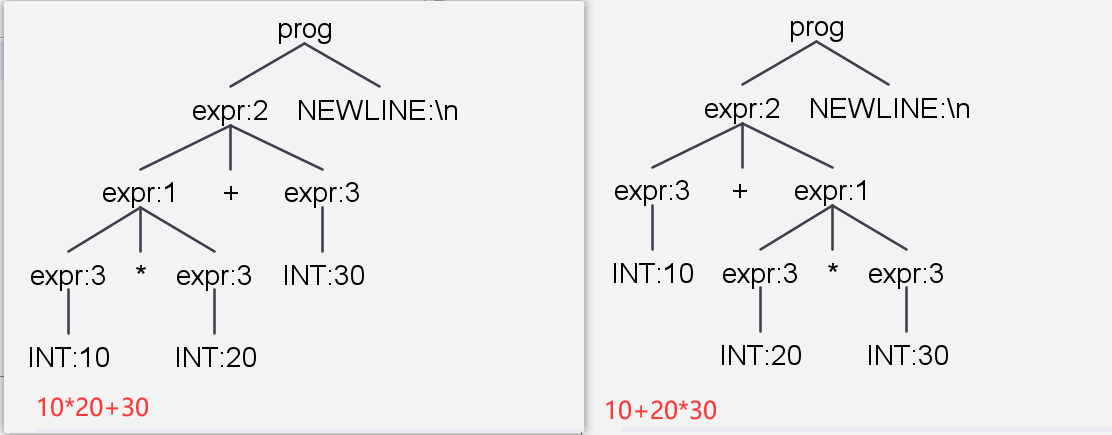
这就是语法分析的结果：语法树。因此，语法分析可以被表述为——从属性字流中根据语法规则构建语法树。

语法分析方法

给定如下的文法（ANTLR格式Test.g4）和字符串

grammar Test;
s : 'a' expr? | 'a';
expr : op 'a' expr?;
op : '+'|'-'|'*'|',';
//字符串: a*a+a

语法分析方法根据文法式的分析途径分为：

自上而下分析方法：从s式开始推导，逐个运用规则得到结果后比较字符串是否符合，最后推导出字符串a*a+a。
自下而上分析方法：从a*a+a开始规约，逐个匹配规则并把字符串规约成规则，最后规约出s式

自上而下

我们将文法规则的候选式展开为文法产生式，去除掉|。例如：S::=A|B展开为S::=A和S::=B。

自上而下分析时，首先构建一个分析栈、一个余留输入串栈与一个分析表

分析栈：初始文法规则入栈。在这个栈里，用于存放匹配文法规则后转化的产生式。
余留输入串栈：输入字符串倒序入栈。当分析栈顶出现了余留输入串栈的栈顶字符的时候，相当于匹配成功，两者共同出栈。
分析表：终结符 X 非终结符规则->文法产生式 的一张表格，当读取余留输入串栈顶时，根据分析栈顶的非终结符选择文法规则产生式。

如下图所示，这里 $\epsilon$ 代表空串。

而设计自上而下分析方法，就是怎么设计分析表。

很明显，自上而下的分析会面临

二义性问题：多个候选式应该怎么选择，以及运算符优先级问题
左递归问题：最左推导时会陷入死循环
回溯问题：如果在某一步无法完成匹配，需要回溯到上一次推导情况

二义性问题引入候选式的优先级设定；左递归问题通过修改文法为右递归来消除；回溯问题需要通过在推导式时，向后预读（lookahead）k个字符进行改善，这样的方法称为LL(k)。

例如LL(1)，即在读取栈顶字符后，还需要再往下读一个字符；下一个字符是出现在下一个文法产生式的首部的（First）、本非终结符规则后（Follow）的终结符首字母。

自下而上

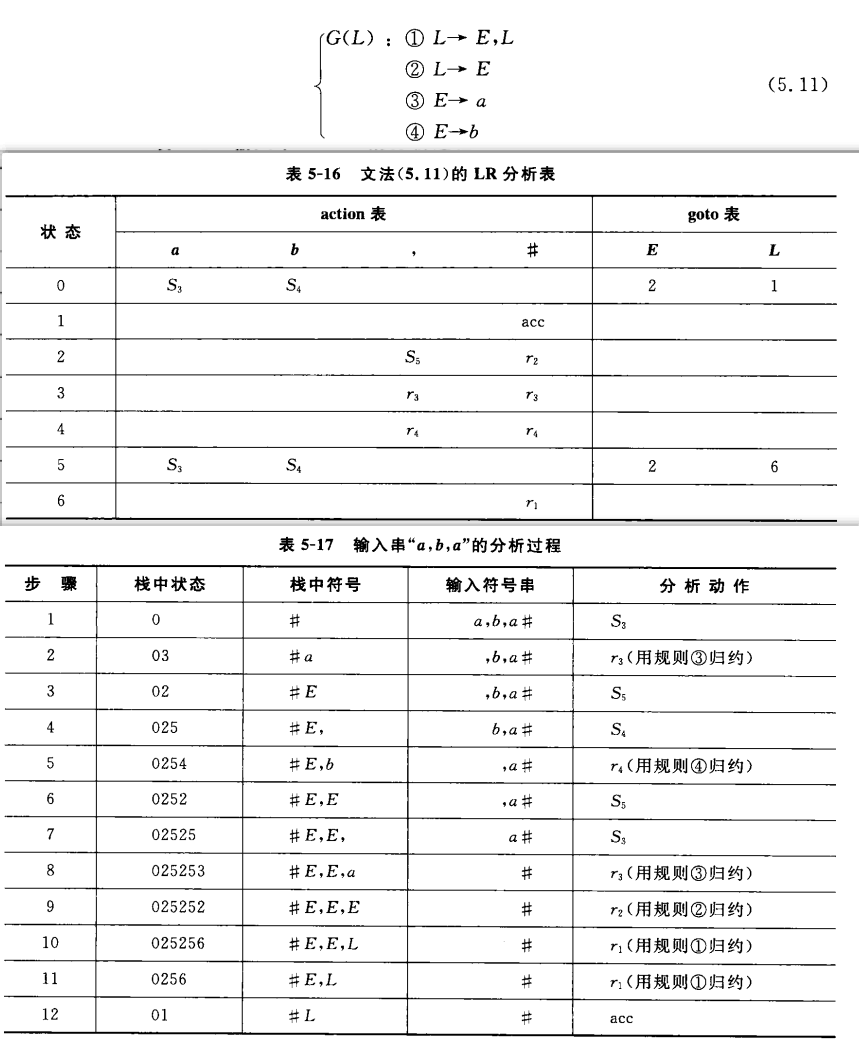
我们将文法规则的候选式展开为文法产生式，并按顺序进行编号。

自下而上分析时，首先构建一个分析栈、一个余留输入串栈与一个分析表。

分析表：
- action表：当前状态为q，输入符号串栈的栈顶输入为a时的行为：
  - 移进：填入状态 $S_n$ ，n为状态序号。移进时，输入符号和状态分别进入分析栈。
  - 规约：规则 $r_n$ ，n为文法产生式编号。规约时，将状态栈、符号栈栈顶都出栈，规约结果入符号栈；规约后，根据当前的状态在goto表中找到转移的状态入状态栈
  - 接受： $acc$
  - 出错
- goto表：当前状态栈栈顶状态为q，符号栈的栈顶E时，需要转移到的状态
分析栈：
- 状态栈：初始时为0状态入栈。
- 符号栈：初始时为空。
余留输入串栈：输入字符串倒序入栈。

分析表的构建

分析表是怎么构建的呢？

LR(0)项目：候选式任何位置添加圆点，点表示规约匹配发生到了哪一步

这些项目可以分为

规约项目：点到了候选式末尾：A->aA·
接受项目：点到了开始符号的候选式末尾S->A·
移进项目：点在终结符中间
待约项目：点到了下一个非终结符前面A->a·A

拓广：如果S有多个候选式，则在开始符号前面加一个S'->S

项目集规范族：很显然，不同的LR(0)项目之间的关系是输入新的符号，点发生了位置变化。这时候我们可以构建一个非确定性有限自动机NFA，将其简化为确定性有限自动机DFA。这个DFA的项目集就是项目集规范族。我们还可以通过假设圆点的移动来构建项目集规范族。例如：S->·A和S->·B和A->·b都是圆点刚刚开始移动的时候，因此属于同一个状态。

项目集规范族数就是状态数，项目集规范族之间如何变化，就是这个表格的填写。可以看到，当输入是非终结符时，填入goto表；当输入是终结符时，填入action表。

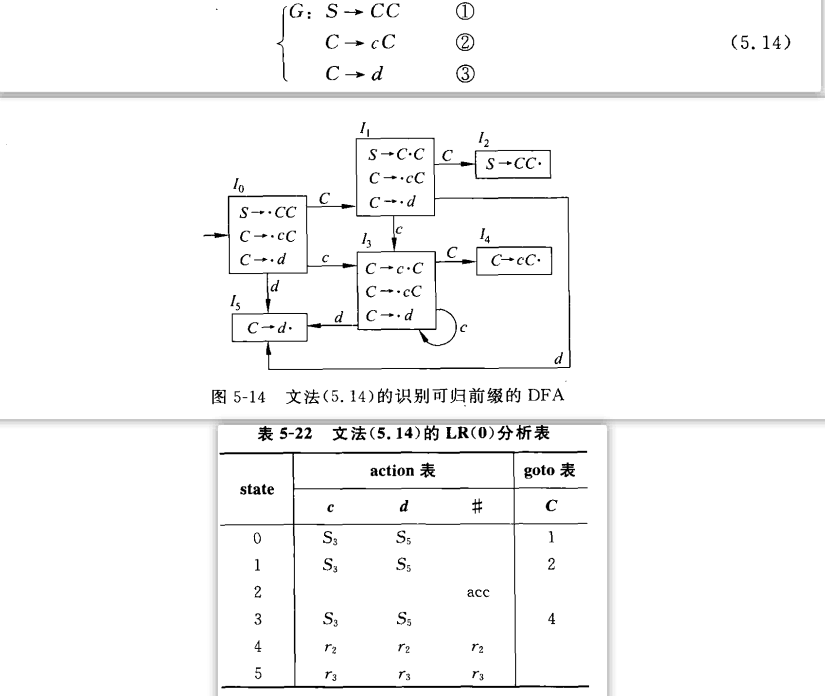
自下而上的方法是无二义性的，但也会面临同一个状态与输入变量时存在既移进又规约；或者多个规约的情况。SLR通过Follow集进行改进，但会面临移进与规约同时存在的问题。LR(k)需要引入搜索符进行判别。LALR(1)则是通过同心项目集改进表格大小，但是会面临规约-规约冲突。

ANTLR的分析方法

ANTLR使用的是自上而下的方法，它称之为LL(*)方法。通过设计策略，从传统的固定k≥1 lookahead扩展到任意lookahead，并最终根据解析决策的复杂性和输入符号进行回溯。具体看以下论文。LL-star-PLDI11.pdf (antlr.org)open in new window

我们回顾一下对于运算符优先级的解释，之前的解释方法是属于LR方法；而ANTLR使用的方法是LL(*)方法，因此我们的解释是错误的，反而更加偏向于LR方法的解释。

编译器工作的基本原理1

# 编译器工作的基本原理1

# 编译器和解释器

# 解释器的工作流程

# 处理形式化文本需要的步骤

# 词法分析

# 插播：文法规则

# BNF文法表示

# ANTLR的词法规则

# 语法分析

# 语法树

# 语法分析方法

# 自上而下

# 自下而上

# 分析表的构建

# ANTLR的分析方法

编译器工作的基本原理1

编译器和解释器

解释器的工作流程

处理形式化文本需要的步骤

词法分析

插播：文法规则

BNF文法表示

ANTLR的词法规则

语法分析

语法树

语法分析方法

自上而下

自下而上

分析表的构建

ANTLR的分析方法